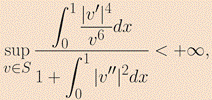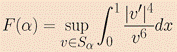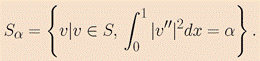Abstract

Carl Sundberg from University of Tennessee-Knoxville conjectured that

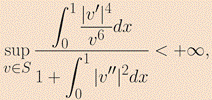
where

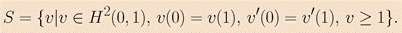
Our goal is to use a computational approach to investigate if (CSI) holds and to compute the related supremum, assuming it is finite. To do so, we observe that the supremum in (CSI) is equal to:

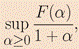
where

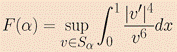
and

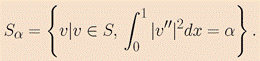
The strategy we advocate at the moment is a pretty crude one, namely, tabulate the function 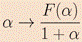in order to get information on the boundedness of the supremum in (CSI). In our lecture, we will discuss the numerical computation of F(alpha), the associated problem of Calculus of Variations being solved by a methodology combining a finite difference discretization and an augmented Lagrangian algorithm associated with the following three families of linear constraints v-q_0=0, v'-q_1 =0 and v''-q_2 = 0.

The results of numerical experiments (with a in the range [0,10^6]) will be presented; we will discuss the conclusions we can draw from them concerning the veracity of (CSI).