|
Research
|
![]()
![]()
![]()
|
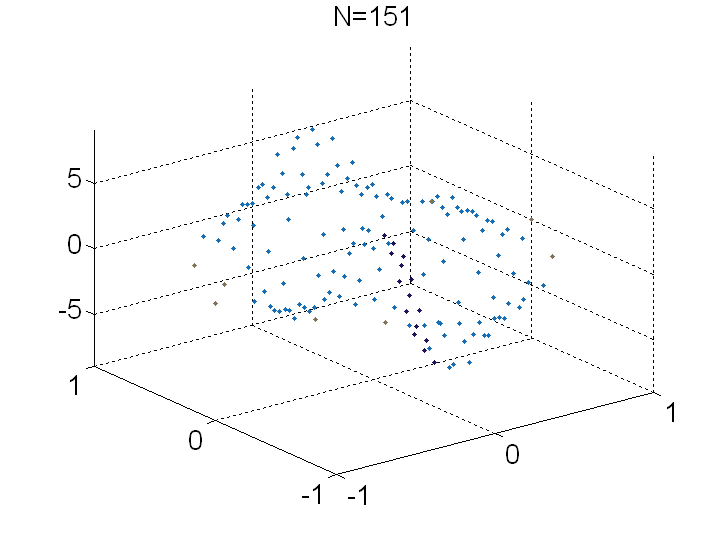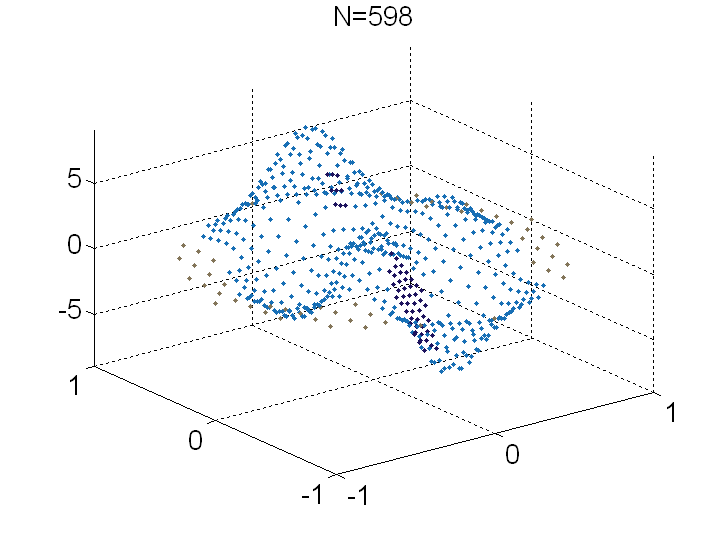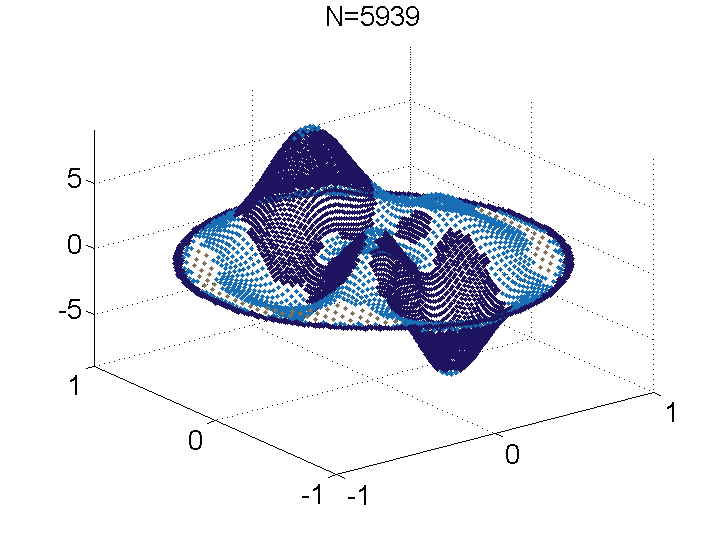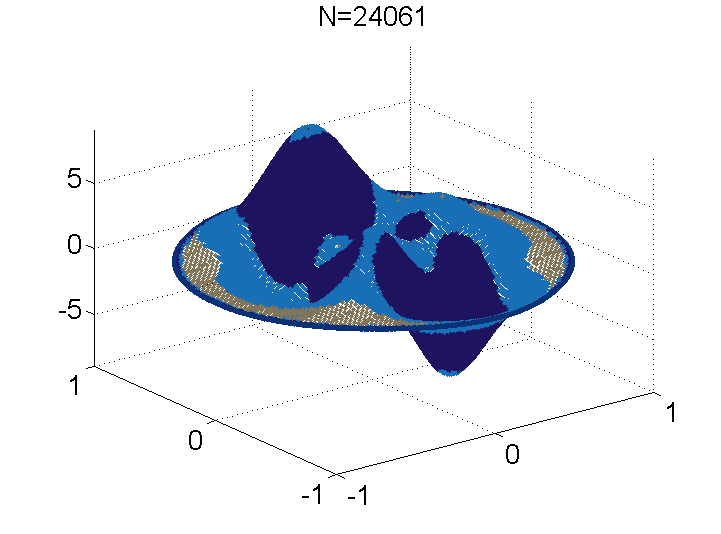
Radial basis functions: A smooth scalar R+ to R function, e.g. Gaussian exp( -r^2 ), which usually is induced from a kernel function, e.g. exp( - || x - z ||^2 ). The set of points Z={ z } is commonly referred to as the RBF centers or trial centers. Nonsymmetric kernel-based collocation methods (Kansa methods): Impressed by the meshfree nature, simplicity to program, dimension independence, and arbitrarily high convergence rates in interpolations, E.J. Kansa proposed to modify the RBF interpolation method to solve PDEs in the early 90s. Using the same linear combinations of RBFs, Kansa imposed strong-form collocation conditions instead of interpolation conditions for identifying the unknown coefficients. Kansa method collocates PDEs at the trial centers Z to yield a square linear system. Though Kansa methods are very successful in a large variety of applications for engineering and science, there were no proven results about them for over 10 years. After many unsuccessful attempts to establish such a foundation, it was revealed that there are extremely rare cases where the original approach fails because the underlying linear system is singular. Solvability: In order to ensure solvability, we proved that overtesting is required. That is, we need some appropriate sets of collocation points X in the domain and Y on the boundary such that |X| +|Y| > |Z|. Error estimates: We found a partial answer to the convergence of overdetermined Kansa formulations. Our analysis was carried out based on the continuous and discrete maximum norms. We showed that the max-norm minimizer of a residual functional converges to the exact solution at the optimal speed, i.e. with the same convergence rate as the interpolant converges to the exact solution. On one hand, it was nice to finally have a convergence theory for Kansa methods. On the other hand, the nonlinear nature of this formulation cannot be handled effortlessly and required a specially designed adaptive algorithm. From then on, we attempted to extend the theories to the least squares minimizer and numerically verified in extended precision arithmetic that the LS minimizer also converges at the optimal rate. Recently, we worked out the necessary assumptions for a class of weighted least-squares algorithms to be convergent. Our main contribution here is the proof of an inverse inequality for kernels in bounded domains. We robustly showed the conditions on the RBF, trial centers in Z, and collocation points in X and Y for our proven error estimates to apply. This allows us to theoretically justify if Kansa methods are suitable for the given problem. Adaptive Greedy Algorithms: As Kansa methods gain popularity, finding appropriate settings becomes another important open question: How can we stably solve severely ill-conditioned linear systems? We proposed a series of sequential-greedy algorithms for selecting quasi-optimal sets of columns (or meshless trial subspaces in Kansa methods) that guarantee stable solutions from meshless methods. They were iterative methods that built up non-singular subsystems by selecting a row, then a column, in some greedy way. The expansion process continues until the problem of ill-conditioning is detected. All these methods can be implemented in a matrix-free fashion, in which only the necessary entries in the matrix are computed and stored, to reduce the storage requirement. The newest result was a block-greedy algorithm. The main challenge is that the greedy strategy does not generalize to block form in a trivial way. Therefore, to properly select multiple rows and columns in each iteration, we propose some economic ways to select/preselect rows and columns. Then, we deploy expansive algorithms on small submatrices to make final selections. By designing with complexity in mind, every iteration of the block-greedy algorithm can be interpreted as a combination of Householder reflections and the Gram-Schmidt process. Other features are added to improve accuracy and robustness. Most importantly, the new algorithm significantly reduces the computational cost from the previous O(k^4+Nk^2) to O(Nk^2) if k columns is selected from an NxN linear system.
miniWIZ (Research Advisor): TURNING OLD PROBLEMS INTO HIGH VALUE LOW-CARBON PRODUCTS
Transforming Human Desire into Earth Saving endeavor, MINIWIZ innovation turns trash into desired products. We create a niche with endless possibility of growth by developing and marketing eco products into different market segments based on new sustainable material technology. As a Creative Partner in Today’s Low Carbon revolution, we transform these innovative materials into real consumer facing commercial products/solutions today
|
![]()
| |
Last
modified on
September 3, 2018
|